DINÁMICA DE POBLACIONES (II): MODELO DE LOTKA-VOLTERRA

En 1925, el biomatemático de Europa del Este, Alfred Lotka, y en 1926 el matemático italiano Vito Volterra, independientemente, propusieron un conjunto de ecuaciones diferenciales  que reflejaban las fluctuaciones de las poblaciones de un depredador y su presa a lo largo del tiempo:

MODELO DE LOTKA-VOLTERRA DE LA RELACIÓN ENTRE DEPREDADOR Y PRESA

ECUACIONES PARA EL MODELO DE DEPREDACIÓN

r1 = Tasa intrínseca de incremento de la presa.

N1 = Densidad de la presa.

N2 = Densidad del depredador.

P*N1*N2 = Pérdidas individuales, a una tasa proporcional a los encuentros del depredador y los individuos presa, debido al producto de la densidad de la presa y del depredador.

P = Coeficiente de depredación.

a = Coeficiente que relaciona los nacimientos del depredador a las presas consumidas.

d2 = Tasa de muerte del depredador.

Fuente: Modelo matemático de gestión de pesquerías

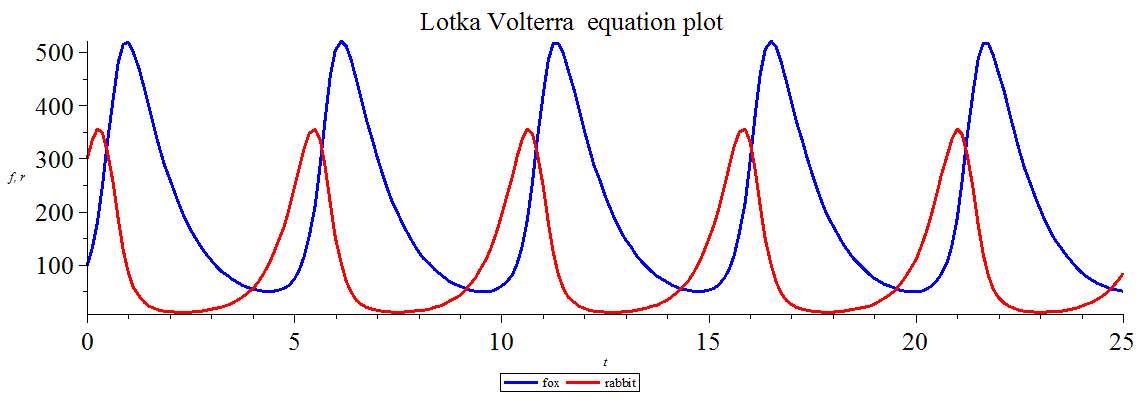
1. Justifica el carácter cuasiperiódico de la gráfica de Lotka-Volterra.

2. Realiza un diagrama de Forrester que represente esta situación. 

Organización y diversidad de la biosfera from Gemita165